The Ultimate Guide To Prime Curves For Peak Performance

What are prime curves?

Prime curves are a family of elliptic curves over finite fields that have been optimized for use in cryptography. They were first introduced by Certicom in 1998, and have since become the most widely used type of curve for elliptic-curve cryptography (ECC).

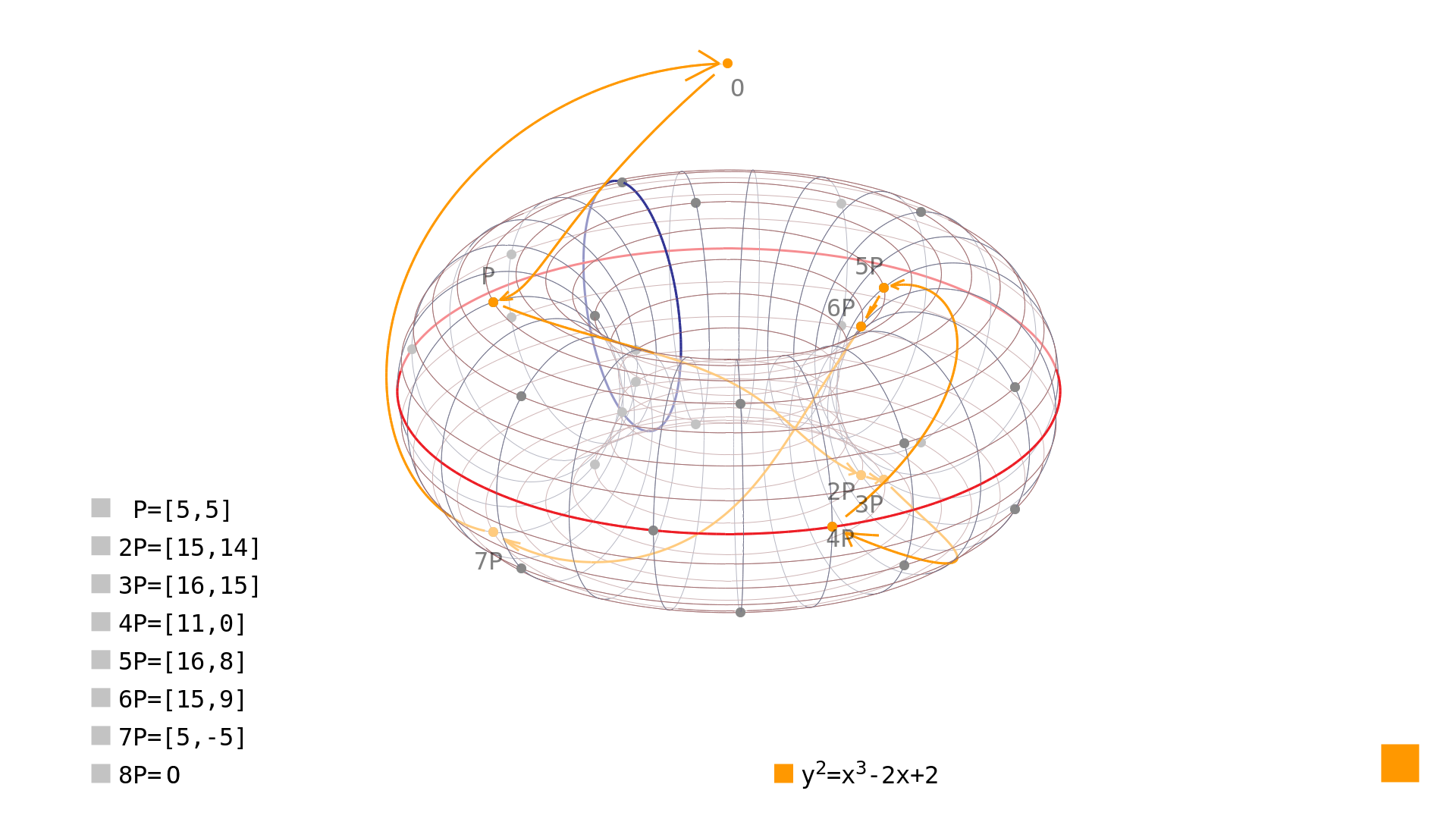
Prime curves are defined by the equation $$y^2 = x^3 + ax + b$$, where a and b are constants. The security of a prime curve is based on the difficulty of finding the discrete logarithm of a random point on the curve. This problem is believed to be computationally infeasible, even for the most powerful computers.

• The Exhusband Of Jessica Dupart A Comprehensive Guide
• The Ultimate Guide To Rhett Hartzog Master Seo Strategies

Prime curves have a number of advantages over other types of curves for ECC. They are relatively easy to implement, and they offer a high level of security. As a result, they are used in a wide variety of applications, including:

Digital signatures Encryption Key exchange

Prime curves are an important part of the cryptographic landscape. They provide a high level of security for a variety of applications, and they are relatively easy to implement.

Prime Curves

Prime curves are a family of elliptic curves over finite fields that have been optimized for use in cryptography. They are used in a wide variety of applications, including digital signatures, encryption, and key exchange.

• Pablo Schreibers Significant Other Meet His Longtime Partner
• Szas Daughter Uncovering Her Age And More

• Definition: y^2 = x^3 + ax + b
• Security: Based on the difficulty of the discrete logarithm problem
• Advantages: Easy to implement, high level of security
• Applications: Digital signatures, encryption, key exchange
• History: Introduced by Certicom in 1998

Prime curves are an important part of the cryptographic landscape. They provide a high level of security for a variety of applications, and they are relatively easy to implement. As a result, they are likely to continue to be used for many years to come.

Definition

The equation y^2 = x^3 + ax + b defines a family of curves known as elliptic curves. Prime curves are a specific type of elliptic curve that is used in cryptography. They are defined over a finite field, and their coefficients a and b are chosen to optimize their security properties.

• Facet 1: The role of coefficients a and b
  

  The coefficients a and b play a crucial role in determining the security of a prime curve. The larger the coefficients, the more difficult it is to solve the discrete logarithm problem on the curve. This makes prime curves more resistant to attack.

• Facet 2: Prime curves in cryptography
  

  Prime curves are used in a wide variety of cryptographic applications, including digital signatures, encryption, and key exchange. They are particularly well-suited for use in embedded devices, such as smart cards and mobile phones, due to their low computational overhead.

• Facet 3: Historical context
  

  Prime curves were first introduced by Certicom in 1998. They have since become the most widely used type of curve for elliptic-curve cryptography.

• Facet 4: Comparison to other curve types
  

  Prime curves offer a number of advantages over other types of curves for cryptography. They are relatively easy to implement, and they offer a high level of security. As a result, they are the most widely used type of curve for elliptic-curve cryptography.

Prime curves are an important part of the cryptographic landscape. They provide a high level of security for a variety of applications, and they are relatively easy to implement. As a result, they are likely to continue to be used for many years to come.

Security

The security of prime curves is based on the difficulty of the discrete logarithm problem (DLP). The DLP is a mathematical problem that is believed to be computationally infeasible, even for the most powerful computers. This means that it is very difficult to find the discrete logarithm of a random point on a prime curve.

• Facet 1: The role of the DLP in cryptography
  

  The DLP is a key problem in cryptography. It is used in a wide variety of cryptographic algorithms, including digital signatures, encryption, and key exchange. The security of these algorithms depends on the difficulty of the DLP.

• Facet 2: The DLP and prime curves
  

  Prime curves are a type of elliptic curve that is particularly well-suited for use in cryptography. This is because the DLP is more difficult to solve on prime curves than on other types of curves.

• Facet 3: The security of prime curves
  

  The security of prime curves depends on the size of the field over which they are defined. The larger the field, the more difficult it is to solve the DLP on the curve. This makes prime curves very resistant to attack.

• Facet 4: Prime curves in practice
  

  Prime curves are used in a wide variety of cryptographic applications, including digital signatures, encryption, and key exchange. They are particularly well-suited for use in embedded devices, such as smart cards and mobile phones, due to their low computational overhead.

Prime curves are an important part of the cryptographic landscape. They provide a high level of security for a variety of applications, and they are relatively easy to implement. As a result, they are likely to continue to be used for many years to come.

Advantages

Prime curves offer a number of advantages over other types of curves for cryptography. They are relatively easy to implement, and they offer a high level of security. This makes them ideal for use in a wide variety of applications, including digital signatures, encryption, and key exchange.

• Ease of implementation
  

  Prime curves are defined by a relatively simple equation, which makes them easy to implement in software and hardware. This is an important advantage for embedded devices, such as smart cards and mobile phones, which have limited computational resources.

• High level of security
  

  Prime curves are resistant to a variety of attacks, including the discrete logarithm problem (DLP). The DLP is a mathematical problem that is believed to be computationally infeasible, even for the most powerful computers. This makes prime curves very secure, even against well-funded adversaries.

• Wide range of applications
  

  Prime curves are used in a wide variety of cryptographic applications, including digital signatures, encryption, and key exchange. They are also used in a number of protocols, such as TLS and SSH. This makes prime curves a valuable tool for securing a wide range of data and communications.

Prime curves are an important part of the cryptographic landscape. They offer a high level of security and are relatively easy to implement. This makes them ideal for use in a wide variety of applications, including digital signatures, encryption, and key exchange.

Applications

Prime curves are used in a wide variety of cryptographic applications, including digital signatures, encryption, and key exchange. These applications are essential for securing data and communications, and prime curves play a vital role in their security.

• Facet 1: Digital signatures
  

  Digital signatures are used to ensure the authenticity and integrity of data. They are created by using a private key to encrypt a hash of the data. Anyone can verify the signature using the corresponding public key. Prime curves are used to generate the public and private keys used in digital signatures.

• Facet 2: Encryption
  

  Encryption is used to protect data from unauthorized access. It is done by using a key to encrypt the data. The data can only be decrypted by someone who has the key. Prime curves are used to generate the keys used in encryption.

• Facet 3: Key exchange
  

  Key exchange is used to establish a shared secret between two parties. This secret can then be used to encrypt communications between the two parties. Prime curves are used to generate the shared secret used in key exchange.

Prime curves are an essential part of the cryptographic infrastructure that protects our data and communications. They are used in a wide variety of applications, and their security is based on the difficulty of the discrete logarithm problem.

History

Prime curves were introduced by Certicom in 1998. This was a significant event in the history of cryptography, as it led to the development of more secure and efficient cryptographic algorithms. Prior to the introduction of prime curves, elliptic curve cryptography (ECC) was not widely used due to the lack of efficient algorithms for implementing ECC on finite fields. Prime curves solved this problem by providing a way to implement ECC on finite fields in a way that was both efficient and secure.

The introduction of prime curves had a major impact on the field of cryptography. ECC is now used in a wide variety of applications, including digital signatures, encryption, and key exchange. Prime curves are also used in a number of protocols, such as TLS and SSH. This makes prime curves a valuable tool for securing a wide range of data and communications.

The introduction of prime curves by Certicom in 1998 was a major milestone in the development of cryptography. Prime curves have made ECC more efficient and secure, and they are now used in a wide variety of applications.

Prime Curves FAQs

Prime curves are a family of elliptic curves over finite fields that have been optimized for use in cryptography. They are used in a wide variety of applications, including digital signatures, encryption, and key exchange. Here are some frequently asked questions about prime curves:

Question 1: What are prime curves?

Prime curves are a family of elliptic curves over finite fields that have been optimized for use in cryptography. They are defined by the equation y^2 = x^3 + ax + b, where a and b are constants.

Question 2: Why are prime curves used in cryptography?

Prime curves are used in cryptography because they provide a high level of security. The security of prime curves is based on the difficulty of the discrete logarithm problem, which is a mathematical problem that is believed to be computationally infeasible.

Question 3: What are some of the applications of prime curves?

Prime curves are used in a wide variety of applications, including digital signatures, encryption, and key exchange. They are also used in a number of protocols, such as TLS and SSH.

Question 4: Who invented prime curves?

Prime curves were introduced by Certicom in 1998.

Question 5: Are prime curves secure?

Prime curves are considered to be very secure. The security of prime curves is based on the difficulty of the discrete logarithm problem, which is a mathematical problem that is believed to be computationally infeasible.

Question 6: What are some of the advantages of using prime curves?

Prime curves offer a number of advantages over other types of curves for cryptography. They are relatively easy to implement, they offer a high level of security, and they are used in a wide range of applications.

Prime curves are an important part of the cryptographic landscape. They provide a high level of security for a variety of applications, and they are relatively easy to implement. As a result, they are likely to continue to be used for many years to come.

Next Article Section: Applications of Prime Curves

Conclusion

Prime curves are a powerful tool for cryptography. They provide a high level of security and are relatively easy to implement. This makes them ideal for use in a wide range of applications, including digital signatures, encryption, and key exchange.

The development of prime curves has been a major milestone in the history of cryptography. They have made ECC more efficient and secure, and they are now used in a wide variety of applications. As the need for secure data and communications continues to grow, prime curves are likely to play an increasingly important role.

Detail Author:

• Name : Prof. Jamar Greenholt MD
• Username : marquardt.keira
• Email : keira.ratke@nolan.biz
• Birthdate : 1989-05-05
• Address : 18368 Sandrine Ridges Bednarberg, DC 08911
• Phone : +1-361-686-9711
• Company : Zulauf, Kihn and Crooks
• Job : Securities Sales Agent
• Bio : Qui itaque repellat at. Est autem minus quo voluptatem. Dolorem provident eos nostrum ad enim.

Socials

twitter:

• url : https://twitter.com/jgoodwin
• username : jgoodwin
• bio : Vitae voluptatibus delectus dolores est atque. Odit laboriosam rem tempore deleniti hic soluta. Consectetur et possimus veniam accusantium ratione esse.
• followers : 5771
• following : 1740

instagram:

• url : https://instagram.com/jonathangoodwin
• username : jonathangoodwin
• bio : Est sed quia eos. Aut aut mollitia quo ut quo blanditiis quis.
• followers : 4851
• following : 462

tiktok:

• url : https://tiktok.com/@jonathan_official
• username : jonathan_official
• bio : Quam accusamus velit minus illum tempore dolorem sint cupiditate.
• followers : 4165
• following : 449

linkedin:

• url : https://linkedin.com/in/jgoodwin
• username : jgoodwin
• bio : Itaque ea ut voluptatem a aut.
• followers : 1498
• following : 1188

facebook:

• url : https://facebook.com/jonathan_goodwin
• username : jonathan_goodwin
• bio : Sit quo rem est sint odio qui. Vitae dolor fuga ullam est voluptatum numquam.
• followers : 6529
• following : 2978